Draw And Label Ray Sr

Segments and rays

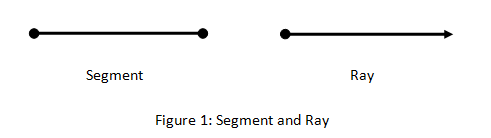
Segments and rays are under the subset of lines. A segment is a part of a line having 2 endpoints and has a item length. On the other hand, a ray is also a part of line having 1 endpoint and the other direction extends indefinitely. Figure one illustrates a segment and a ray.

Segment-Ray

Terms to recall

Congruent
- having the aforementioned size and shape.
Distance
- a numerical value that describes how far 2 objects are.
Endpoint
- a point located at the end role of a segment, defining its limit.
Opposite
- opposite in position or direction.
Subset
- a portion of a set.
Vertical
- upwards-down position.

Definition of a Segment

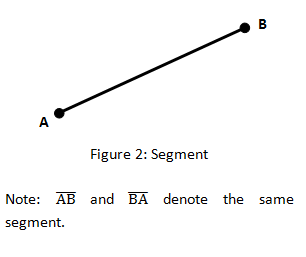
A segment is a set of points consisting of 2 points of the line called the endpoints, and all of the points of the line between the endpoints. It is commonly used to correspond the length, height, or width of a certain object and the distance betwixt two objects. It is named by using the label of its endpoints and insert a line (( ) ̅) above the messages. Figure 2 shows segment AB which can also be written as (AB) ̅.

Segment

Example 1

Draw (CD) .

Respond:

two-point-label

Explanation:

Draw two points and label it as C and D.

Connect the 2 points straight each other.

Case 2

How many segments are at that place in the line below?

Answer : 6

line-endpoints

Explanation:

Employ the points in the line as endpoints of the segments.

The segments are (QR) , (RS) , (ST) , (QS) , (RT) , and (QT) .

Midpoint of a Segment

A midpoint of a segment is the bespeak that divides the line segment into two congruent parts. It is located at the centre of the segment. Figure 3 shows the midpoint of a segment.

Midpoint

Note: The two vertical lines indicate that the distances from the midpoint to both endpoints are equal.

Case iii

The length of (XY) is 12 and Z is the midpoint of (XY) . Discover the length of (XZ) .

Answer: 6

Explanation:

The midpoint Z divides (XY) into two congruent parts: (XZ) and (YZ) .

The length of (XZ) is ½ the length of (XY) which is ½ 12 = six.

Example 4

O is the midpoint of (NP) . If (NO) = 9, what is the length of (NP) ?

Answer: xviii

Explanation:

The midpoint O divides (NP) ̅ into 2 congruent parts: (NO) ̅ and (PO) ̅.

sThe length of (NP) ̅ is twice the length of (NO) ̅ which is 2 9 = 18.

Addition and Subtraction of Segments

Figure 4 illustrates iii collinear points Due east, F, and G forming a segment.

Three-Collinear-Points

Points E and Yard constitute the endpoints of the segment which is (EG) and point F in betwixt divides (EG) into two segments: (EF) and (FG) . The sum of the lengths of (EF) and (FG) is equal to the length of (EG) . Therefore, (EF) + (FG) = (EG) . The expression represents a segment if indicate F is betwixt Points E and G.

The post-obit expressions are also truthful for the lengths of the segments:

(EF) = (EG) – (FG)

(FG) = (EG) – (EF)

Case 5

Find the length of (JL) in the figure.

Points-J-L-are-endpoints

Answer: 10

Explanation:

Points J and Fifty are endpoints of (JL) and point K is between points J and L.

Therefore, (JK) + (KL) = (JL) .

(JL) = vi + four = ten.

Example half-dozen

The length of (UV) is 13 and W is between points U and V. If (WU) = 5, what is the length of (VW) ?

Answer: 8

Points U and Five are endpoints of (UV) and betoken Westward is between points U and 5.

Therefore, (UW) + (VW) = (UV) .

(UW) = (WU) = 5

And so, (VW) = (UV) - (UW) = 13 – 5 = viii.

Definition of a Ray

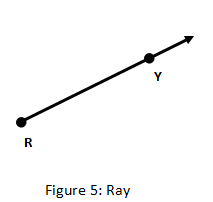
A ray consists of a betoken on a line and all points on one side of the bespeak. Information technology has only ane endpoint. Rays are commonly used in physics to announce direction and besides force. In naming a ray, consider two points in the ray: one is the endpoint and the other is any point in the ray. The characterization of the endpoint should be the start letter of the proper name of the ray and identify a correct arrow sign ( ( ) ) above the letters. Effigy 5 illustrates a ray labeled equally (RY) .

ray

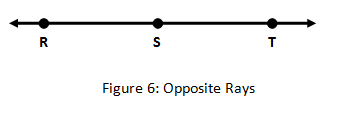
Contrary rays are two rays that prevarication on the aforementioned line having a common endpoint and no other point in mutual. In Figure 6 shown, (RS) ̅ and (ST) ̅ are opposite rays.

Opposite-rays

Example 7

Draw (AE) .

Answer:

two-point-label

Explanation:

Describe 2 points and labeled information technology as A and E.

Connect the two points straight each other and extend the line from betoken E.

Case 8

Observe the number of rays that can be found in the line.

Answer:

Explanation: 12

Consider ii points in the line as the points of the ray.

Rays pointing to the right tin be named as (MB) , (BP) , (PC) , (MP) , (BC) , and (MC) .

Rays pointing to the left tin can exist named as (CP) ,(Lead) , (BM) , (CB) , (PM) , and (CM) .

There are 12 rays that are institute in the line.